Event

Graduate Seminar
Relaxation of mean curvature flow via the parabolic Ginzburg-Landau equation
Mariel Saez
7 Nov 2006, 17:00 – 19:00

I will discuss a method to represent sets evolving under mean curvature flow as nodal sets of the limit of solutions to the parabolic Ginzburg-Landau equation, given by $\be \frac{\partial u_\epsilon}{\partial t}-\Delta u_\epsilon +\frac{(\nabla_u W)(u_\epsilon)}{2\epsilon ^2}=0.\ee$ . More specifically, first I will consider a curve evolving under curve shortening flow and a potential function with two minima at and . Then I will show that there are solutions $u_\epsilon$ to equation (*) that as $\epsilon \to 0$ , satisfy

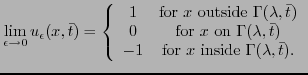
$\displaystyle \lim_{\epsilon\to 0}u_\epsilon(x,\bar{t})=\left\{\begin{array}{cc... ...{t}) \\ -1& \hbox{for $x$ inside }\Gamma(\lambda,\bar{t}). \end{array} \right.$

Then I will show that similar results can be proved for networks of curves evolving under curve shortening flow. I will also discuss some corollaries that can be derived from this representation.

http://geometricanalysis.mi.fu-berlin.de/os/os-ws0607.htm

Individual Session of:

Graduate Seminar: Oberseminar Analysis, Geometry and Physics (Winter Term 2005/06)

Related to:

Activities 2006